Radius of the Fresnel zone is given by
[math]Rf=(v/2)(t_0/f_\mathrm{dom})^{1/2}[/math]
where v: velocity of layer
[math]t_0[/math]: two way travel time
[math]f_\mathrm{dom}[/math] :dominant frequency in the spectrum
This shows that high frequencies give better resolution than lower frequencies and resolution deteriorates with depth and increasing velocities.
However I found some text in “Seismic Data Analysis- Yilmaz” which is contradictory.
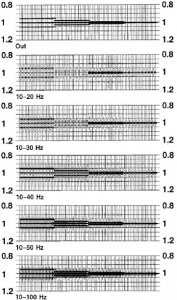
“Just having low or high frequencies does not improve temporal resolution. Both low and high frequencies are needed to increase temporal resolution. This is demonstrated further in Figure 1.1-30.”
Could someone explain what the author is trying to say here or am I making a mistake in interpretation somewhere ?
This was a question on StackExchange, see the question here.
In seismic data analysis, we have to distinguish between vertical (temporal) and horizontal resolution.
The (First) Fresnel zone is linked to the vertical resolution and defines the area in which the collected energy will still stack constructively.
The temporal resolution, however, defines what the wave “sees”. The events can still be resolved if their thickness is within a fourth of the wavelength (lambda). However, in some cases it can go down to (lambda / 32). This is a matter of detectability of events.
Don’t forget that we’re dealing with superpositions of different frequencies so basically low frequencies will give use the necessary energy content of general trends while high frequencies enable us to make a distinction between geologic features.
This file from the university of Oslo gives a nice overview.
(The picture is from a blog post I’ve written on knowing your wavelength it’s CC-BY-SA Source1 Source2
from EarthScience Stackexchange
Jesper Dramsch
Latest posts by Jesper Dramsch (see all)
- Juneteenth 2020 - 2020-06-19
- All About Dashboards – Friday Faves - 2020-05-22
- Keeping Busy – Friday Faves - 2020-04-24